Frequenzweiche berechnen - Hochpass und Tiefpass
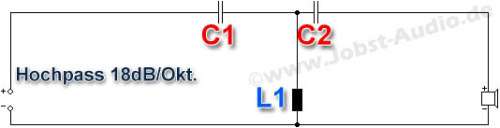
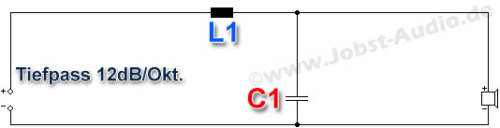
| Hochpass: | Tiefpass: | ||||
| Flankensteilheit: | dB/Okt | Flankensteilheit: | dB/Okt | ||
| Filtercharakteristik: | Filtercharakteristik: | ||||
| Impedanz: | Ω | Impedanz: | Ω | ||
| Xover HP: | Hz | Xover TP: | Hz | ||
| Bauteile: | Bauteile: | ||||
| L1 | mH | L1 | mH | ||
| L2 | mH | L2 | mH | ||
| L3 | mH | L3 | mH | ||
| C1 | µF | C1 | µF | ||
| C2 | µF | C2 | µF | ||
| C3 | µF | C3 | µF | ||
| Für einen Bandpass (typisch für Mehrweg-Boxen am Mitteltöner) wird einfach ein Tiefpass mit einem Hochpass kombiniert, wobei der TP idR. als erstes Glied in der Kette steht. 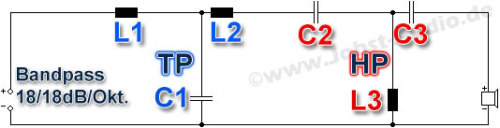 Die Flankensteilheit wird als Ordnung/Order bezeichnet, so entspricht eine Flankensteilheit von 6dB/Okt einem Filter der 1. Ordnung, 24dB/Okt entsprechend 4. Ordnung. Je höher die Ordnung: - Um so weiter wird die Phase gedreht. - Um so steiler die Flanke. - Um so weniger Tiefe, bzw. hohe Frequenzen werden durchgelassen. - Um so geringer die lineare Auslenkung des Chassis bei XO* * Von Chassis, Parameter, Auslegung und Gesamtabstimmung abhängig! Filtercharakteristiken: Linkwitz-Riley: Weist im Ggs. zum Butterworth keine +3dB bei der Übernahmefrequenz auf. Butterworth: Flacher Verlauf im Durchlassbereich, guter Kompromiss-Filter. Bessel: Sehr gute Gruppenlaufzeit und lineare Phase, dafür recht flache Flanke im Durchlassbereich. Chebychev: Im Durchlassbereich steile Flanke, die Gruppenlaufzeit leidet darunter allerdings stark. Solen Split: Veränderter Butterworth, hat im Ggs. den Übergangpunkt bei -6 dB anstatt -3dB. Legendre: Kompromiss zwischen Butterworth und Chebychev-Filter. Gauss: Konstante Gruppenlaufzeit im Durchlass- und Sperrbereich, zudem gute Sprungantwort ohne Überschwinger, bei gleichzeitig steiler Flanke. Linear Phase: Der Phasenverlauf entspricht hier der linearen Funktion der Frequenz, konstante Gruppenlaufzeit. |


